Physique de l'infiniment grand : Une introduction à la relativité générale par et pour des amateurs

PACT 12

Professeurs :

Matthieu Vilatte (Chapitres 1 à 7) Centre de Physique Théorique, Ecole Polytechnique, FRANCE & Institut de Physique Théorique, Université Aristote de Thessalonique, GRECE
Paul Ramond (Chapitres 8) Centre de recherche en mathématiques de l'Université Paris-Dauphine, FRANCE

Pré-requis

Théorie des champs classiques (cours PAT11)

Bibliographie

Pour la partie "physique":

David Langlois, Introduction à la relativité générale, poly de l'X empruntable à la BCX
P. Marios Petropoulos, Relativité générale, poly de l'X empruntable à la BCX
Robert Wald, General relativity, University of Chicago Press
Matthias Blau, Lecture Notes on General Relativity, University of Bern, voir sa page web
R. Taillet, Introduction à la relativité générale, cours en podcast de l'université de Savoie (youtube)

Pour la partie "géométrie":

Olivier Biquard, Géométrie différentielle, Notes du DMA de l'ENS Ulm
Mikio Nakahara, Geometry, topology and physics, CRC Press
Will J. Merry, Differential Geometry, ETH Zurich, voir sa page web

Organisation

9 séances de 3 heures : 2h à 2h15 de cours / 45' à 1h de travaux dirigés
8 devoirs maisons à rendre en début de chaque séance composés d'un ou deux exercices de travaux dirigés à rédiger.

Programme détaillé et prévisionnel du cours

Chapitre 1 : un peu d'histoire
Théorie newtonienne de la gravitation
- Espace absolu dans lequel l'invariant est la longueur pythagoricienne
- Temps absolu, simultanéité selon Newton
- Invariance sous le groupe de Galilée
- Gravitation newtonienne : 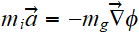avec
Relativité restreinte (rappels brefs de PAT)
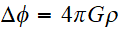
- Invariance sous le groupe de Lorentz
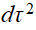
- Espacetemps décrit par Minkowski, invariant $d\tau^{2}$
- Rappel sur la structure du cone de lummière
Vers la relativité générale
- Expérience de pensée d'Einstein, la lumière ressent la gravité
- Expérience de pensée de Schild, il faut considérer des espaces temps courbes
- Principe d'équivalence : formulation
  - Poisson <=> Einstein
  - Espace affine <=> Variété différentielle
- Conséquences du principe d'équivalence: nécessité de concevoir des espaces courbes
- La covariance généralisée
Quelques dates Objectif du cours
- Description de la théorie relativiste de la gravitation par la formulation mathématique du principe d'équivalence
- Établissement des équations de la dynamique de l'espacetemps
- Étude de quelques applications de ces équations
Complément: l'équation de Poisson
- Rappels sur les distributions
- Notion de fonction de Green d'un opérateur
- Démonstration de Poisson pour une distribution de masse

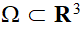
Chapitre 2 : un soupçon de géométrie
Géométrie en espaces affines
- Définition, coordonnées cartésiennes et métrique
- Les vecteurs, leur décomposition et leur loi de transformation contravariante
- Les covecteurs, leur décomposition et leur loi de transformation covariante
- Dualité vecteurs/covecteurs avec la métrique
- Les tenseurs : définition, propriétés
Variétés différentielles
- Notion d'espace topologique séparé, d'atlas puis de variété, l'exemple de $S^{2}$
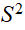
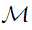
- Notion de champ scalaire sur une variété $\QTR{cal}{M}$
- Espace tangent, vecteur 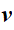$\QTR{bs}{v}$ tel que
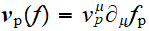
- Fibré tangent et champs de vecteurs
- Espace cotangent, forme 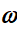$\QTR{bs}{\omega}$ telle que
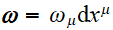
- Fibré cotangent et champs de covecteurs
- Tenseurs et champs de tenseurs
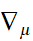
Dérivation covariante $\nabla_{\mu}$
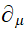
- Perte du caractère tensoriel par la dérivation $\partial_{\mu}$
- Notion de transport parallèle sur la sphère
- Relation entre la dérivation covariante et le transport parallèle
- Construction de 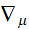$\nabla_{\mu}$ : règle de Liebniz, linéarité, action sur un scalaire, action sur un vecteur
- Emergence des symboles de connexion avec le transport parallèle
- Action sur un tenseur
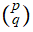
- Courbure et torsion d'une connection quelconque
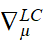
Connexion de Levi-Civita $\nabla^{LC}_{\mu}$
- Tenseur métrique, variété riemanienne, signature
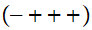
- Propriétés de la connexion de Levi-Civita (lc) : sans torsion, métrique compatible
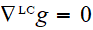
- Unicité de la connexion de LC
- Symboles de Christoffel à partir de la métrique
Géodésiques : le mouvement des particules libres
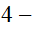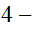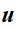- vitesse et accélération : $\QTR{bs}{u}$ tel que 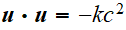le photon (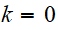), les particules massives (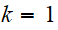), 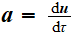soit
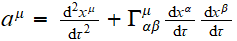
- Courbes auto-parallèles
- Notion de paramètre affine
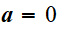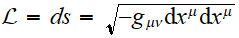- Equation géodésique : à partir de $\QTR{bs}{a}=0$ , avec le lagrangien , ou le lagrangien 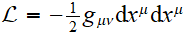en paramétrage affine. Conclusion et remarques. Exemple de la métrique de Milne.
- Mouvement des corps en relativité générale
Bilan de la description mathématique de l'espacetemps
- Nécessité d'une variété riemanienne de signature 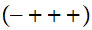munie d'une connexion de Levi-Civita et dont les géodésiques sont les trajectoires suivies par les corps
Complément: les hypersurfaces

Chapitre 3 : la courbure et la matière
La courbure
- Tenseur de courbure de Riemann : définition géométrique et lien avec le transport parallèle
- Propriété des différentes composantes, identités de Bianchi
- Tenseur de Ricci, courbure scalaire
- Noyau de la dérivée covariante de Levi-Civita : 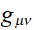$g_{\mu\nu}$ par définition, 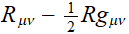par le calcul
Contenu physique des quantités mathématiques
- Que deviennent les composantes de la métrique à basse énergie
- Etude d'une plaque tournante dans un champ de gravité : contenu physique de la connexion affine
- Contenu physique du tenseur de Riemann
La matière comme source des équations d'Einstein
- La matière est décrite par un tenseur : covariance généralisée
- Quelles sont les caractéristiques de ce tenseur ? Rang 2, symétrie
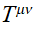
- Construction phénoménologique de $T^{\mu\nu}$
- Conservation de la matière :
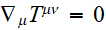
- Exemple du fluide parfait
- Remarques sur la définition 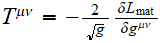et exemple du tenseur du champ de Klein Gordon
Les équations de champ d'Einstein (1915)
- Obtenue "à la physicienne", courbure égale matière mais la matière est dans le noyau de la dérivée covariante que l'on a déjà étudié.
- Notion de constante cosmologique
- Limite basse énergie pour $\chi$

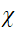
Chapitre 4 : la solution de Schwarzschild (1916)
Dérivation de la métrique
- Stationnarité, staticité et symétrie sphérique
- Hypothèses statiques et symétrie sphérique : forme la plus générale
- Calcul de la solution et remarque sur les coordonnées
Symétries et constantes du mouvement
- Théorème de Noether appliqué à
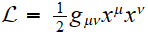
- Comment trouver les quantités associées ?
- Vecteurs de Killing et application à la métrique de Schwarzschild
- Equation radiale en fonction des paramètres conservés
Géodésiques de genre temps
- Calcul de l'avance du périhélie de Mercure
Géodésiques de genre lumière
- Calcul de la déviation des rayons lumineux
- Eclipse de 1919
Deux autres tests de la relativité générale
- Effet Shapiro
- Rougissement gravitationnel
Complément: le théorème de Birkhoff
- La solution de Schwarzschild est l'unique solution sous les hypothèses de staticité et symétrie sphérique.

Chapitre 5 : Astrophysique stellaire relativiste
Hypothèses
- Métrique statique et symétrie sphérique
- Le contenu matériel : fluide parfait barotropyque
Résolution des équations d'Einstein
- Conservation du fluide
- Conditions aux limites
- Système TOV
- Comparaison avec le cas newtonnien
Le cas de la densité constante
- Masse maximale d'un astre relativiste
- Théorème de Buchdahl
Compléments
- Objets compacts en astrophysique
- D'autres résultats sur les masses maximales en RG

Chapitre 6: les trous noirs
Différents types de singularité
- Singularité de coordonnées: peut être enlevée via un changement de carte
- Singularité de courbure: s'observe dans les invariants comme le carré du Riemann
- Schwarzschild: que se passe-t-il en ?
Horizon des évènements et complétude géodésique
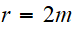- Notion d'horizon des évènements: nulle lumière ne sort de la région intérieure
- Complétude géodésique en paramétrage affine
Coordonnées de Kruskal
- Construction de la carte de Kruskal
- Le diagramme de Kruskal
Compléments
- Quelques mots sur Kerr, Reisneer-Noström, Kerr-Newmann
- Quelques théorèmes sur les trous noirs
- Quelques mots sur les diagrammes de Carter-Penrose

Chapitre 7 : un peu de cosmologie
Principe cosmologique
- Observations (CMB, expansion, propriétés des grandes structures de l'Univers,...)
- Enoncé du principe cosmologique
- Conséquence : métriques FLRW
- Distance physique / distance comobile
- Rougissement cosmologique
Equations de la dynamique de l'Univers dans le cadre du principe cosmologique
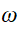
- Contenu matériel : le fluide parfait barotropique d'indice $\omega$
- Equations de Friedmann
Evolution cosmologique
- Le big-bang : la singularité dans le passé
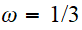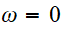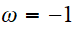
- Solutions pour $\omega=1/3$ , $\omega=0$ et $\omega=-1$
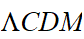
Quelques mots sur $\Lambda CDM$
- Les paramètres cosmologiques
- La nécessité d'une constante cosmologique
- Matière noire et énergie sombre
Compléments
- Quelques mots sur les univers de Bianchi

Chapitre 8 : Les ondes gravitationnelles
Ce chapitre sera traîté par Paul Ramond, le contenu est donné à titre purement indicatif.
Linéarisation des équations d'Einstein
- Hypothèses et calcul
- Liberté de jauge et sa fixation
- Equation d'onde ayant 2 polarisations
Conséquences physiques
- Emission d'ondes gravitationnelles
- Formule du multipôle et le système binaire
- Détection des ondes gravitationnelles (LIGO-VIRGO)

Physique de l'infiniment grand : Une introduction à la relativité générale par et pour des amateurs

PACT 12

Professeurs :

Pré-requis

Bibliographie

Organisation

Programme détaillé et prévisionnel du cours

Chapitre 1 : un peu d'histoire

Chapitre 2 : un soupçon de géométrie

Chapitre 3 : la courbure et la matière

Chapitre 4 : la solution de Schwarzschild (1916)

Chapitre 5 : Astrophysique stellaire relativiste

Chapitre 6: les trous noirs

Chapitre 7 : un peu de cosmologie

Chapitre 8 : Les ondes gravitationnelles